石墨烯振动模式
一些词汇含义
前两篇文章,波动方程求解中
本征值
$$sin\sqrt{\lambda} l=0$$
此时,$\lambda$ 只能取特定的值,称为 本征值
$$\lambda _n = (\frac{n\pi}{l})^2 \qquad n = 0,1,2,3……$$
给定边界条件(两端位移为0),特定时刻,绳子可以有很多满足条件的分布(波谷的个数不同),每个分布中,绳子的波谷个数 $n$ 不同,$\lambda$ 与 $n$ 相关
本征函数
对于每一个本征值 $\lambda_n$对应一个$X_n(x)$的解
$$X_n(x)=Csin\frac{n\pi}{l}x \qquad n = 0,1,2,3……$$
这个解,被称为 本征函数
给定边界条件(两端位移为0),特定时刻,绳子可以有很多满足条件的分布,每个分布函数都是本征函数
本征频率
对于每一个 $\lambda _n$ 都有一个 $T_n(t)$ 的解与之对应
$$T_n(t)=A_nsin(a\frac{n\pi}{l}t) + B_ncos(a\frac{n\pi}{l}t) \qquad n = 0,1,2,3……$$
此时令 $a\frac{n\pi}{l}=\omega_n$,这里的 $\omega_n$ 就是 本征频率,上面的式子可以写成
$$T_n(t)=A_nsin(\omega_nt) + B_ncos(\omega_nt)\qquad n = 0,1,2,3……$$
绳子上某一点,随时间的位移变化频率
线性代数中
参考 维基百科
本征向量与本征值
$$Av=\lambda v$$
一个 $n \times n$ 矩阵 $A$ 与 $n \times 1$ 矩阵 $v$ 相乘,等于常数 $\lambda$ 与 矩阵 $v$ 相乘,
官方:对于一个给定的方阵 $A$ ,它的特征向量 $v$ 经过这个线性变换之后,得到的新向量仍然与原来的 $v$ 保持在同一条直线上,但其长度或方向也许会改变。
$\lambda$ 为其本征值(eigenvalue,也译本征值、固有值); $v$ 为本征向量(eigenvector),也译“特征向量、固有向量”
举例
如果一个矩阵通过线性变换可以变为对角矩阵
$$
A =\left[
\begin{matrix}
2 & 0 & 0 \
0 & 2 & 0 \
0 & 0 & 4
\end{matrix}
\right]
$$
特征值 就是2和4。2对应的 特征向量 是所有形同 $(a, b, 0)^T$ 的非零向量,而4对应的特征向量是所有形同 $(0,0,c)^{T}$ 的非零向量。2对应的特征空间是一个2维空间,而4对应的特征空间是一个1维空间
构建一维链模型
- 固定边界条件
(0) - (1) - (2) - ….. - (i-1) - (i) - (i+1) - ….. - (n-1) - (n) - (n+1)
(0) 和 (N+1) 两端固定,中间一共N个原子,(-)代表原子之间弹簧连接,以向右为正,第i个原子的位移为 $x_i$,由于固定边界条件,$x_0=x_{n+1}=0$,对于原子(1)收到的力为 $F=-k\Delta x$
$$m\ddot{x_1}=-k(x_1-x_0)+k(x_2-x_1)$$
$$
\frac{m\ddot{x_1}}{k} = x_0+x_2-2x_1=
\left[
\begin{matrix}
x_1 & x_2 & … & x_{i-1} & x_i & x_{i+1} & … & x_{n-1} & x_n
\end{matrix}
\right]
\dot{}
\left[
\begin{matrix}
-2 \ 1 \ … \ 0 \ 0 \ 0 \ … \ 0 \ 0
\end{matrix}
\right]
$$
矩阵(行列式)相乘:左行 $\times$ 右列,每一项相加
同理,对于第i个原子,
$$
\frac{m\ddot{x_i}}{k} = x_{i-1}+x_{i+1}-2x_i=
\left[
\begin{matrix}
x_1 & x_2 & … & x_{i-1} & x_i & x_{i+1} & … & x_{n-1} & x_n
\end{matrix}
\right]
\dot{}
\left[
\begin{matrix}
0 \ 0 \ … \ 1 \ -2 \ 1 \ … \ 0 \ 0
\end{matrix}
\right]
$$
第n个原子
$$
\frac{m\ddot{x_n}}{k} = x_{n-1}+x_{n+1}-2x_n=
\left[
\begin{matrix}
x_1 & x_2 & … & x_{i-1} & x_i & x_{i+1} & … & x_{n-1} & x_n
\end{matrix}
\right]
·
\left[
\begin{matrix}
0 \ 0 \ … \ 0 \ 0 \ 0 \ … \ 1 \ -2
\end{matrix}
\right]
$$
又因为x与时间的关系为余弦函数,
$$x_i=A_i cos(\omega t + \phi) $$
$$\ddot{x_i}=-\omega^2(A_i cos(\omega t + \phi))=-\omega^2 x_i$$
将上面n个式子相加,并代入$\ddot{x_i}=-\omega^2 x_i$
$$
-\omega^2\frac{m}{k}\vec{x} = \vec{x} V
$$
其中:
$$
\vec{x} =
\left[
\begin{matrix}
x_1 & x_2 & … & x_{i-1} & x_i & x_{i+1} & … & x_{n-1} & x_n
\end{matrix}
\right]
$$
$$
V=
\left[
\begin{matrix}
-2 & 1 & … & 0 & 0 & 0 & … & 0 & 0\
1 & -2 & … & 0 & 0 & 0 & … & 0 & 0\
… & … & … & … & … & … & … & … & … \
0 & 0 & … & -2 & 1 & 0 & … & 0 & 0 \
0 & 0 & … & 0 & -2 & 1 & … & 0 & 0 \
0 & 0 & … & 0 & 1 & -2 & … & 0 & 0 \
… & … & … & … & … & … & … & … & … \
0 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & 1 \
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -2 \
\end{matrix}
\right]
$$
正好和之前的本征向量、本征值形式相同
$$Av=\lambda v$$
$v=\vec{x}, A=V, \lambda=-\omega^2\frac{m}{k}$
$V$ 矩阵已知,可以求解特征向量 $\vec{x}$(n维),特征值为 $-\omega^2\frac{m}{k}$
求解出来的特征值有n个,每个特征值对应一个特征向量 $\vec{x}$(n维)
使用python求解代码如下:
1 | # 特征值赋值给tzzs,对应特征向量赋值给tzxls |
二维石墨烯
类似,按照FPU本征模式计算本征矩阵
$$
V_{mn}=
\left\lbrace
\begin{matrix}
-24 \gamma & m=n\
-12 \gamma & mn两个原子近邻\
-2 \gamma & mn两个原子次近邻 \
0 & 其他情况
\end{matrix}
\right.
$$
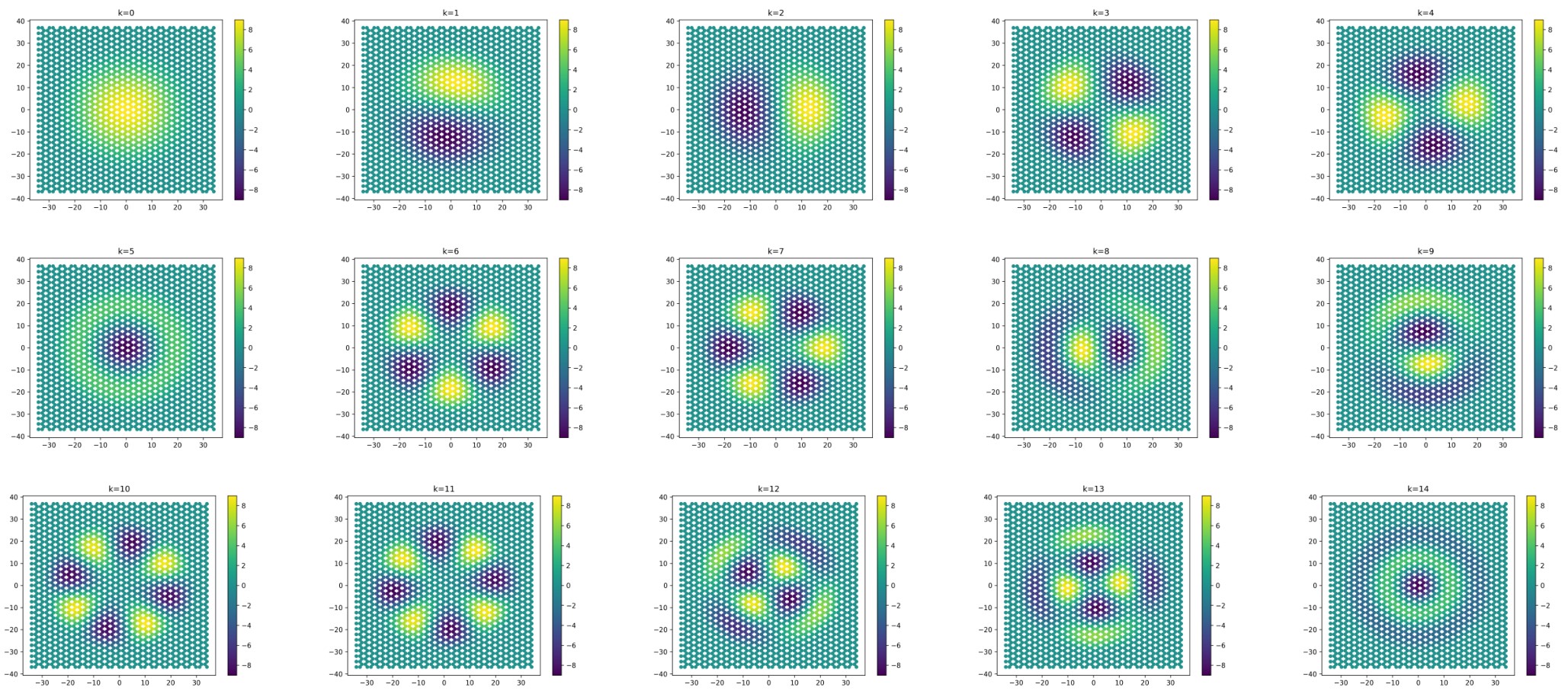
本征值排序以后,前15个本征模式如图
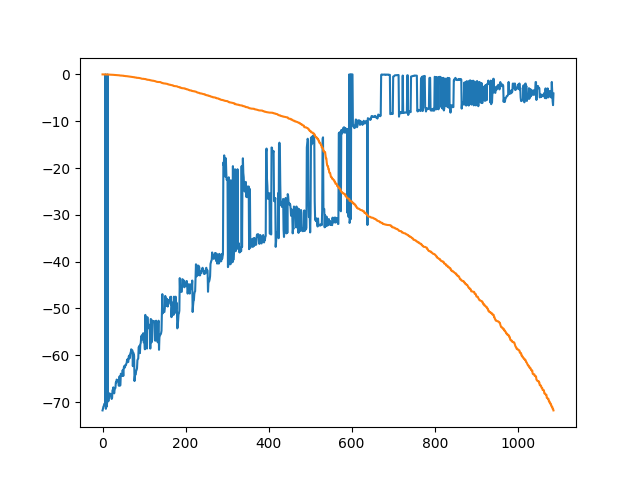
本征值(橙色排序后,蓝色排序前)
画图方法:取第一个本征向量,扩大一定倍数,做为石墨烯的z轴坐标,用scatter画图,z轴数值同时作为scatter的颜色
本文作者:yuhldr
本文地址: [https://yuhldr.github.io/posts/45586.html](https://yuhldr.github.io/posts/45586.html)
版权声明:转载请注明出处!