波动方程求解
大量参考《数学物理方法》-杨孔庆
弦振动推导波动方程
高中竞赛物理常见近似,x趋近于0时,如下(画个三角形显而易见):
$$cos x = 1 $$
$$ sin x = tan x \times cos x = tanx = x(弧度制)$$
初始设定
弦:线密度 $\rho$,每一点上下震动(x方向唯一为0)
受力分析
x处,dx长的的一段绳子(线密度$\rho$):
受到三个可能的力,两端的拉力$T_x$和$T_{x+dx}$,与绳子相切,切角大小分别为$\alpha$和$\beta$,并且单位长度弦可能受到外力,暂时认为是竖直方向,$f_0(x,t)$
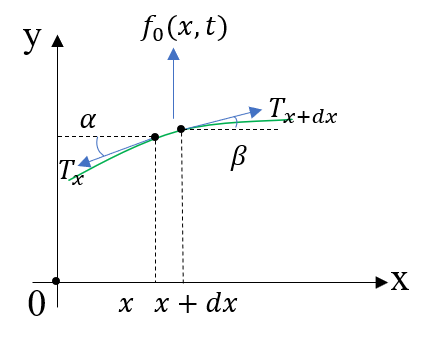
由于x轴上没有运动,x方向受力平衡
$$T_xcos\alpha - T_{x+dx} cos\beta = 0$$
弦的振幅很小,可取$\alpha$$\beta$ -> 0,由上面的近似可得
$$T_x = T_{x+dx} = T$$
竖直方向上,运动方程为
$$Tsin\alpha-T_{x+dx}sin\beta+f_0(x,t)dx=ma=(\rho dx) u_{tt}$$
其中$u_{tt}$为竖直方向位移对时间的二阶导数
由最开始的近似关系,可进一步化简为:
$$ Ttan\alpha-Ttan\beta+f_0(x,t)dx=(\rho dx) u_{tt} $$
$tan$函数可以看做斜率:
$$Ttan\alpha-Ttan\beta=T(\frac{\partial u}{\partial x}\bigg|_{x+dx}-\frac{\partial u}{\partial x}\bigg|_x)$$
其中
$$\frac{\partial u}{\partial x}\bigg|_{x+dx} - \frac{\partial u}{\partial x}\bigg|_x=\frac{\partial^2 u}{\partial^2 x}dx$$
可得$$T\frac{\partial^2 u}{\partial^2 x}+f_0(x,t)=\rho u_{tt}$$
写成标准形式:
$$u_{tt}-au_{xx}=f(x,t)$$
其中 $a=\frac{T}{\rho}$,即振动在弦上传播的速度,$f(x,t)=\frac{f_0(x,t)}{\rho}$被称为外力密度,单位长度密度上所施加的外力。当$f(x,t)=0$,方程变为
$$u_{tt}-a^2u_{xx}=0 (0<x<l,t >0)$$
即为一次齐次波动方程
定解条件
“初始条件”与“边界条件”
初始条件
位移分布和速度分布已知,$\psi(x)$和$v(x)$为已知函数
$$u(x,0)=\psi(x) \qquad 0 \leq x \leq l$$
$$u_t(x,0)=v(x) \qquad 0 \leq x \leq l$$
边界条件
共三类,分别是:
- 绳子两端固定
- 绳子两端不收到任何力,自由端
- 绳子两端是弹簧
固定边界(两端)
好比最上面的那个图,两端始终在x轴上的某一点即
$$u(0,t)=u(l,t)=0$$
随着时间t的变化,x=0和x=l处的绳子两端坐标u不变
自由边界(两端)
在我们之前的方程推导中,默认的是,$x$处的绳子长度$dx$,受到绳子两端的其他绳子拉力为
$$T_x、T_{x+dx}$$
$y$轴方向的受力,x轴方向一律认为不动
$$T_xsin\alpha、T_{x+dx}\beta$$近似以后为
$$T_xsin\alpha = Ttan\alpha = T\frac{\partial u}{\partial x}\bigg|_x$$
$$T_{x+dx}sin\beta = Ttan\beta = T\frac{\partial u}{\partial x}\bigg|_{x+dx}$$
而真实情况是,$x=0$和$x=l$处,绳子自由时,这两段绳子只能受到一端绳子的力,另一端外力为0,即
$$T\frac{\partial u}{\partial x}\bigg|_0=0$$
$$T\frac{\partial u}{\partial x}\bigg|_l=0$$
其中T可以去掉(绳子两端一个外力左下,一个右上,方向不同,但是此处为0,不考虑正负号)
$$\frac{\partial u}{\partial x}\bigg|_0=0$$
$$\frac{\partial u}{\partial x}\bigg|_l=0$$
弹性边界(两端)
绳子在两个竖直的弹簧上系着,在这种情况下,2中的竖直方向外力不为0,认为是一种弹力,类似于弹簧$f=au$,其中a为弹簧系数,u为y轴竖直方向位移,平衡时,两端受力为(暂时认为向上的力为负):
$$-\frac{\partial u}{\partial x}\bigg|_0 + a_1u(0,t) = 0$$
$$\frac{\partial u}{\partial x}\bigg|_l + a_2u(l,t) =0$$
两边弹簧弹性系数不一样,分别为$a_1$,$a_2$。
本文作者:yuhldr
本文地址: [https://yuhldr.github.io/posts/58883.html](https://yuhldr.github.io/posts/58883.html)
版权声明:转载请注明出处!