FPU单链选择定则

发表于 更新于 分类于 阅读次数： 本文字数： 1.6k 阅读时长 ≈ 6 分钟
FPU $\beta$ 模型，32个原子，固定边界条件，各个模式能量被激活规律

前两篇，已经模拟计算了单链 $\alpha \beta$ 两种模型，并且复现了 $\alpha$模型的FPU经典图，接下来，在 $\beta$ 模型下推导选择定则，并且做相关模拟验证。

推导

$N+1$ 个原子，两端原子固定，中间 $N$ 个非线性弹簧连接，

$$x_0 (t)=\dot{x}0(t)= x{N}(t) = \dot{x}_N (t)=0$$

第j个原子受力（$j=1,2,…,N-1$）

$$
\begin{aligned}
F_j =& [(x_{j+1}-x_{j})-(x_j-x_{j-1})] \
&+ \alpha [(x_{j+1}-x_{j})^2-(x_j-x_{j-1})^2] \
&+ \beta[(x_{j+1}-x_{j})^3-(x_j-x_{j-1})^3]
\end{aligned}
$$

哈密顿量为：

$$
H=\sum_{j=1}^{N}\left[\dot{x}{j}^{2} / 2+\left(x{j}-x_{j-1}\right)^{2} / 2+\alpha\left(x_{j}-x_{j-1}\right)^{3} / 3+\beta\left(x_{j}-x_{j-1}\right)^{4} / 4\right]
$$

上面的推导可参见 相关文章

$\beta$模型下，3次项可出现正负，令$\alpha=0$

对于固定边界条件，谐振子来说解为

$$x_j = i\sum_{k=1}^{N}\frac{a_k}{\omega_k} e^{\frac{-i\pi j}{N}}$$
其中

$$\omega = 2 sin(\frac{\pi k}{2N})$$

这里，因为是固定边界条件，只看实数部分，即为初始状态振幅，$x_j=\cos{\frac{\pi}{N}j}$，J从0取到N，正好初始状态时，“拱形”固定边界条件

$$
x_{j}-x_{j-1}=i\sum_{k=1}^{N}\frac{a_k}{\omega_k} e^{\frac{-i\pi j}{N}} - i\sum_{k=1}^{N}\frac{a_k}{\omega_k} e^{\frac{-i\pi (j-1)}{N}}= i\sum_{k=1}^{N}\frac{a_k}{\omega_k} e^{\frac{-i\pi j}{N}}(1-e^{\frac{-i\pi}{N}})
$$

$$
\begin{aligned}
\sum_{j=1}^{N}\left(x_{j}-x_{j-1}\right)^{4}=& \sum \frac{a_{k} a_{k’} a_{k’’} a_{k’’’}}{\omega_{k} \omega_{k’} \omega_{k} \omega_{k’’’}} \exp \left[-i \pi j\left(k+k’+k’’+k’’’\right) / N\right] \
& \times[1-\exp (i \pi k / N)]\left[1-\exp \left(i \pi k’ / N\right)\right] \
& \times\left[1-\exp \left(i \pi k’’ / N\right)\right]\left[1-\exp \left(i \pi k’’’ / N\right)\right] \
=& \sum a_{k} a_{k’} a_{k’’} a_{k’’} \exp \left[-i \pi\left(j-\frac{1}{2}\right)\left(k+k’+k’’+k’’’\right) / N\right]
\end{aligned}
$$

上面方程最后一步化简：

已知$\omega_k = 2sin(\frac{\pi k}{2N})$，令 $\frac{\pi k}{2N}=y$

可得
$$
\begin{aligned}
&1-\exp (i \pi k / N)\
&=1-[cos(2y)+isin(2y)]\
&=1-[1-2sin(y)^2+i2sin(y)cos(y)]\
&=2sin(y)[sin(y)-icos(y)]\
&=\omega_k (-i)[cos(y)+isin(y)]\
&= -i \omega_k e^{iy}\
&=-i \omega_k e^{i\frac{\pi k}{2N}}
\end{aligned}
$$
则

$$
\begin{aligned}
&\frac{[1-\exp (i \pi k / N)]\left[1-\exp \left(i \pi k’ / N\right)\right] \times\left[1-\exp \left(i \pi k’’ / N\right)\right]\left[1-\exp \left(i \pi k’’’ / N\right)\right] }{\omega_k \omega_k’ \omega_k’’ \omega_k’’’}\
&=(-i)^4 e^{i\pi \frac{1}{2N}(k+k’ + k’’ + k’’’)}
\end{aligned}
$$

实数部分只有余弦项

$$
\sum_{j=1}^{N} \cos \left[\frac{(j-\frac{1}{2})(k+k’+k’’+k’’’) \pi}{N}\right]=N \cdot D\left(k+k’+k’’+k’’’\right)
$$

因此 k为整数时，有

$$
D(0)=1 \quad D(\pm 2N)=-1 \quad D(*)=0
$$

$$
\sum_{j=1}^{N}\left(x_{j}-x_{j-1}\right)^{4}=N \sum a_{k} a_{k’} a_{k’’} a_{k’’’}D\left(k+k’+k’’+k’’’\right)
$$

$$
H=(N / 2) \sum\left[\left(\dot{a}{k} / \omega{k}\right)^{2}+a_{k}^{2}\right]+(\mu N / 4) \sum a_{k} a_{k’} a_{k’’} a_{k’’’}\left(k+k’+k’’+k’’’\right)
$$

求导得

$$\ddot{a}{k}=-\omega{k}^{2} a_{k}-\mu \omega_{k}^{2} \sum_{k’ k’’ k’’’} a_{k’} a_{k’’} a_{k’’’} D\left(k+k’+k’’+k’’’\right)
$$

欧拉公式可推出 $\cos x = \frac{e^{ix}+e^{-ix}}{2}$
$$
\begin{aligned}
&=\sum_{j=1}^{N} \cos \left[\left(j-\frac{1}{2}\right)\left(k+k’+k’’+k’’’\right) \pi / N\right] \
&=\sum_{j=1}^{N} \cos[\frac{(2j-1)k \pi}{2N}] = \sum_{j=1}^{N} \frac{e^{i\frac{(2j-1)k \pi}{2N}} + e^{-i\frac{(2j-1)k \pi}{2N}}}{2}\
&=a_1 \frac{(1-q^n)}{1-q} + a_1’\frac{(1-q’^n)}{1-q’}
\end{aligned}
$$

其中，$q=e^{\pm \frac{ik\pi}{N}}$， $q=1$的时候即为$2N \quad 0$

等比数列以后为（忽略分母2）：
$$ \begin{aligned}
&=e^{i\frac{k \pi}{2N}}\frac{(1- e^{ik\pi})}{1-e^\frac{ik\pi}{N}}+e^{-i\frac{k \pi}{2N}}\frac{(1- e^{-ik\pi})}{1-e^\frac{-ik\pi}{N}}
=e^{i\frac{k \pi}{2N}}(\frac{(1- e^{ik\pi})}{1-e^\frac{ik\pi}{N}})+e^{i\frac{k \pi}{2N}}\frac{(1- e^{-ik\pi})}{e^\frac{ik\pi}{N}-1}\
&=e^{i\frac{k \pi}{2N}}(\frac{(1- e^{ik\pi})-(1- e^{-ik\pi})}{1-e^\frac{ik\pi}{N}})=e^{i\frac{k \pi}{2N}}(\frac{e^{-ik\pi}- e^{ik\pi}}{1-e^\frac{ik\pi}{N}})\
&=e^{i\frac{k \pi}{2N}}(\frac{\cos{(-k\pi)}+i\sin(-k\pi)- (\cos{(k\pi)}+i\sin(k\pi))}{1-e^\frac{ik\pi}{N}})\
&=e^{i\frac{k \pi}{2N}}\frac{-2i\sin{k\pi}}{1-e^\frac{ik\pi}{N}}
\end{aligned}
$$

$\therefore$ 只要 $k$ 为整数，求和即为0

这个方程的含义是，整个势能项，是由多个模式（$k k’ k’’ k’’’$）组合而成，其中（$k’ k’’ k’’’$）是原有模式，$k$是被原有模式激发起来的新模式，模式的取值为 $1、2、……、N$

$$
\sum_{j=1}^{N}\left(x_{j}-x_{j-1}\right)^{4}=N \sum a_{k} a_{k’} a_{k’’} a_{k’’’}D(k+k’+k’’+k’’’)
$$

假设激发了 $k_0=1$ 模式，也就是初始状态是按照第一个模式分布的，因此初始各个模式的振幅只有第一个不为0： $a_{k_0} \neq 0$

如果上面这个方程不为0，由于 $a_{k} a_{k’} a_{k’’} a_{k’’’}$ 的存在，其中每一项都不能是0，因此$k’=k’’=k’’’=k_0$，$k$被原有模式激发，也不为0
$$
D(0)=1 \quad D(\pm 2N)=-1 \quad D(*)=0
$$
由于上面这个式子，$D(k+k’+k’’+k’’’)$ 这个函数不为 $0$，只能是 $k+k’+k’’+k’’’$ 为 $2N$ 的倍数，注意 $k=-k$

如果，初始激发模式为 $k_0=3=k’=k’’=k’’’$，那么，下一个被激发的模式只能是 $9-3-3-3$，即 $k=9$，再接下来 $15-3-3-9$，即 $k=15$，接下来：$21 \quad 27$

模拟

$\beta$ 模型，其实前两篇blog已经做了模拟，改一下参数就行，现在验证 $\beta$ 模型下，激发第3个模式，看看各个模式能量分布。

代码又重新改了一下，整体上和前两个bolg的差不多，一共三个文件，直接点击打开可能乱码，其实打开以后右键保存，是没有乱码的，编码用的 utf-8，在 ubuntu2004、python3.8 下测试

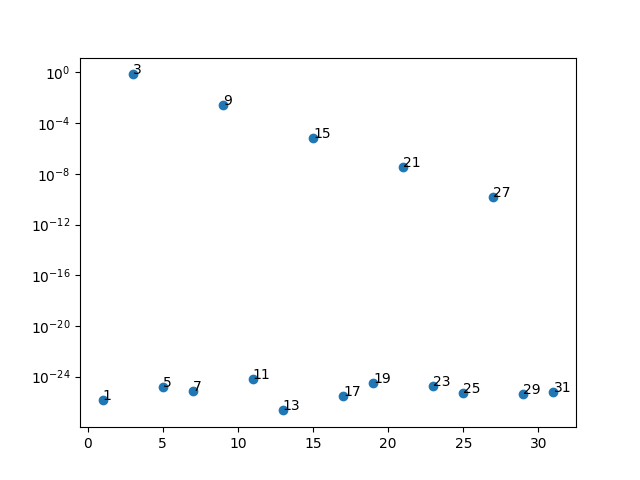
$\beta$模型，奇数模式能量

可以看到，与推测的一致：初始激发3模式，然后9、15、21、27被激发

参考文献

  • Nonlinear coupled oscillators: Modal equation approach

    10.1016/0021-9991(73)90169-1

  • q -Breathers and the Fermi-Pasta-Ulam Problem

    10.1103/PhysRevLett.95.064102

本文作者：yuhldr
本文地址： [https://yuhldr.github.io/posts/53634.html](https://yuhldr.github.io/posts/53634.html)
版权声明：转载请注明出处！