声子态密度计算
声子态密度说明
先理解一下声子态密度（PDOS）吧：
定义：单位频率间隔内的状态数(振动模式数目)
它与声子色散（PDC）关系是有关系的，前面一节，已经给出了色散关系的求解方法（虽然最后我也有点懵）
- 色散关系其实就是每个波失对应的频率
- 声子态密度是，每个频率的声子对应的概率
两者其实仅仅是横纵坐标交换，可以看这里，描述的挺形象的：态密度（PDOS）曲线和声子色散曲线（PDC）的联系 - Joe ZhouMan's blog
一般情况下，计算声子态密度就可以了，因为色散关系的线条实在是太多了（3N个：3个光学枝，3(N-1)个声学支），以石墨烯为例，每个晶胞2个原子，所以是6条线，但是如果要画石墨烯的，就太可怕了，随着直径增加，就太多了
- 高频声子，更容易热输运
一般情况，我是通过 LAMMPS 进行分子动力学模拟的，可以输出每一步某些或全部原子的速度、位置等信息，所以接下来，通过原子速度计算比较方便 所用到的是 Computer Simulation of the Lattice Dynamics of Solids
\[ PDOS(\omega)=\int \frac{<\sum_{i} v_{i}\left(t_{0}\right) \cdot v_{i}\left(t_{0}+t\right)>}{<\sum_{i} v_{i}\left(t_{0}\right) \cdot v_{i}\left(t_{0}\right)>} e^{-2 \pi i \omega t} d t \]
主要使用这里的代码：
参考这些
计算文件以及说明
文件说明
我这里给一个已经测试过的、可以运行的代码，不用管代码什么意思，先运行了再说，里面包含 matlab 和 python 的代码，大致说一下运行逻辑
点我下载 pdos，文件解压以后，共6个文件
4040CNT_20nm.in
lammps脚本文件
BNC.tersoff
势能文件
4040CNT_20nm.data
模型文件：20nm 长的碳纳米管，结构为
m=n=40Rebuild_data.m
matlab函数：处理lammps生成的速度、位移文件
find_pdos.m
matlab函数：计算pdos以及速度自关联函数
plot_pdos.m
matlab主函数：直接运行，计算声子态密度
pdos.py
python函数，计算声子态密度，与matlabb效果一直，并且部分中文注释
4040CNT_20nm.in 整个模拟是 20nm 长的碳纳米管，结构为 m=n=40，模拟分3个阶段（4个run）：
- 松散100000步；
- 平衡100000步
- 然后输出5000步的原子（只有中间的 8-12nm 的纳米管部分）坐标速度信息（用来计算pdos）；
- （与pdos无关，已经注释掉）非平衡模拟1500000步得到热整流系数
模拟计算步骤
LAMMPS运行脚本
4040CNT_20nm.in1
lmp -in 4040CNT_20nm.in
这将会得到3个文件：
- log.4040CNT_20nm.txt：日子
- log.lammps：日志
- 4040CNT_20nm_voutput_all.lammpstrj：第三个run5000步，输出的了中间8-12纳米的原子的速度位移坐标
使用 4040CNT_20nm_voutput_all.lammpstrj 计算 pdos
如果你用的是matlab：其中
*.m结尾的matlab代码，运行plot_pdos.m即可如果你和我一样喜欢开源的python，运行
pdos.py即可，部分注释我用了中文，容易看一些1
python pdos.py
计算的是整体声子如果要计算某一个方向的，修改引用的速度，python文件153行
这将得到4个文件
4040CNT_20nm_voutput_all.npy：
4040CNT_20nm_voutput_all.lammpstrj的txt文件保存为numpy的文件，方便读取，速度会快几十倍4040CNT_20nm_voutput_all_vacf.npy：归一化的速度自关联函数数据
4040CNT_20nm_voutput_all_pdos.npy：pdos 数据
pdos.pdf：使用上面这个文件画出的分子态密度图
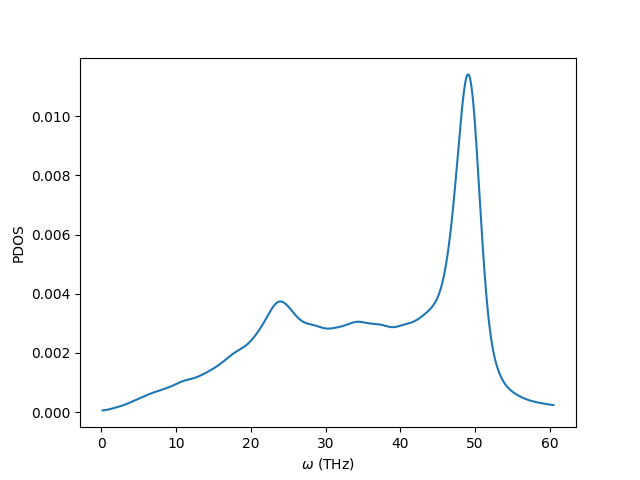
cnt热导率高，从声子角度来看，主要为高频声子，与这里基本上是对应的Enhancement of heat conduction in carbon nanotubes filled with fullerene molecules
本文作者：yuhldr
本文地址： https://yuhldr.github.io/posts/d5c2f773.html
版权声明：转载请注明出处！