声子与色散关系复习-预习
理解不够,后续再学习补充
回顾色散关系求解过程
先说单链的色散关系,与之前波动方程求解类似,再大致说一遍,如图单链
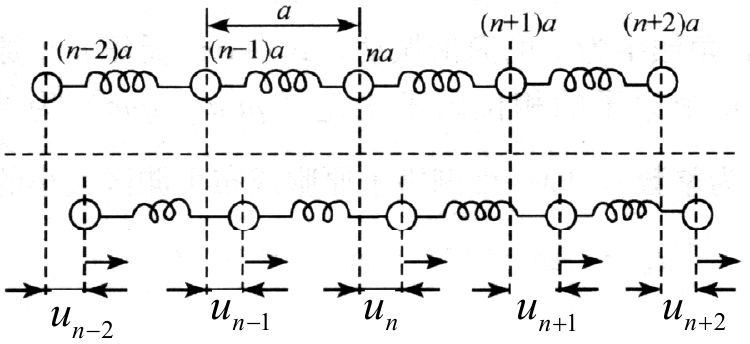
第n原子的位移为 $u_n$,之间的势能关系
$$ F_n=\beta (u_n-u_{n-1} + u_{n+1}-u_n)$$
运动方程为:
$$F=ma \rightarrow m\frac{d^2u_n}{dt^2}=\beta(u_{n+1}+u_{n-1}-2u_{n})$$
这样的线性齐次方程求解为
$$u_{nq}=Ae^{i(\omega t-naq)} \qquad q=\frac{2\pi}{\lambda}$$
$q$ 是波数,意思就是,位移与时间的关系有很多个解,$q$ 可以取整数 $1,2,3,…$,$n$ 指得还是第几个原子,具体为什么,看 波动方程求解2-分离变量法
$\omega$ 是角频率,$\lambda$ 是波长
如果再把这个方程代回运动方程,可以得到
$$\omega=2\sqrt{\frac{\beta}{m}}|sin\frac{1}{2}aq|$$
这个就是色散关系,可以看到原子频率与 $n$ 无关,也就是说,所有原子以相同频率振动,区别仅仅是相位差,相邻原子的相位差为 $qa$
通常把 $\omega$ 与 $q$ 的关系成为色散关系
对于均匀弹性介质,运动方程为
$$\frac{d^2u}{dt^2}=\frac{E}{\rho}\frac{\partial^2u}{\partial x^2}$$
可以得到色散关系为
$$\omega=\sqrt{\frac{E}{\rho}}q$$
需要注意的是,这是格波,$x$只能取$na$格点位置的孤立值
格波的物理意义
前面求解中格波
$$u_{nq}=Ae^{i(\omega t-naq)}$$
原子振动以波的形式在晶体中传播,波的周期为 $\frac{2\pi}{q}$,即,原子相距 $\frac{2\pi}{q}$ 时具有相同的振幅和相位
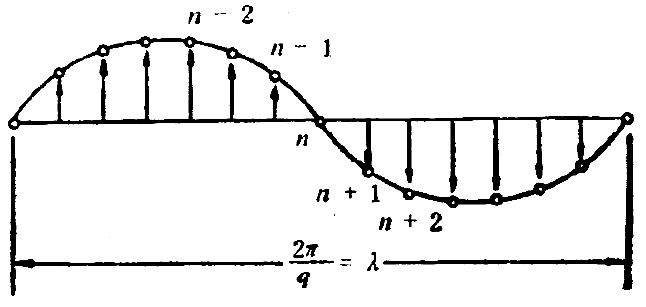
这里的波数 $q=q+\frac{2\pi}{a}\times m$
一维链的第一布里渊区即
$$-\frac{\pi}{a}< q < \frac{\pi}{a}$$
第一布里渊区指得就是,像上面那个图一样,这些原子正好完成一个完整的振动周期
这个方程 $u_{nq}=Ae^{i(\omega t-naq)}$ 和 $\omega=2\sqrt{\frac{\beta}{m}}|sin\frac{1}{2}aq|$可以看到
- n固定,也就是只看某一个原子,q确定以后,随着时间t的变化,变化为正弦函数,改变q意味着,振动频率加快
- t固定,也就是某一时刻,看整个链的原子,也是个正弦函数,波数q也就意味着,整个链也会由一个完整周期变为2个周期、3个周期、……、q个周期
布里渊区
布里渊区一般在倒易空间,什么意思呢,其实就是$2\pi$除以现实中的向量,好处是后面的计算不至于波长出现无限
现实中的晶格之间向量为 $\vec{a}_1 \quad \vec{a}_2$,倒格子中的向量为 $\vec{b}_1 \quad \vec{b}_2$,他们的关系是
$$\vec{b}_i \times \vec{a}j = 2\pi \delta{ij}$$
$$\delta_{ij}=\begin{cases}
1 &(i=j)\
0\quad &(i\neq j)
\end{cases}$$
色散关系图解
前面求解出来 $\omega=2\sqrt{\frac{\beta}{m}}|sin\frac{1}{2}aq|$,如果把图画出来
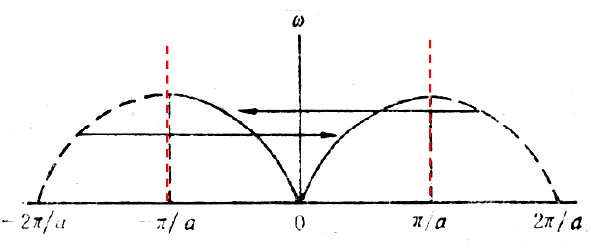 ,
,
常见词
- 波长 ($\lambda$),一个周期的长度
- 波数 ($q$或$k$):每2$\pi$长度有多少个波长 $q=\frac{2\pi}{\lambda}$:”角频率是单位时间内的角度变化,而波数为单位长度内的角度变化,因此波数即是空间上的角频率。波数对应矢量为波矢”。
- 波包:点波包,看维基百科的动图
- 群速度:波包传播的速度
- 相速度,相位传播的速度,两个的区别在于,很多波不是完全大小一样的,把几个大小不同的波放一块是一个波包,这个波包的传递速度是群速度,无论大波还是小波,都有相位,比如都有波峰,而波峰的速度就是相速度,这个不太好理解,点我看动图,所以一般相速度大于群速度
- 长波极限:波数$q \rightarrow 0$即波长无穷大
- 声学支:$q\rightarrow 0 \quad \omega \rightarrow 0$,只有三个,也就是对应整体的三个自由度
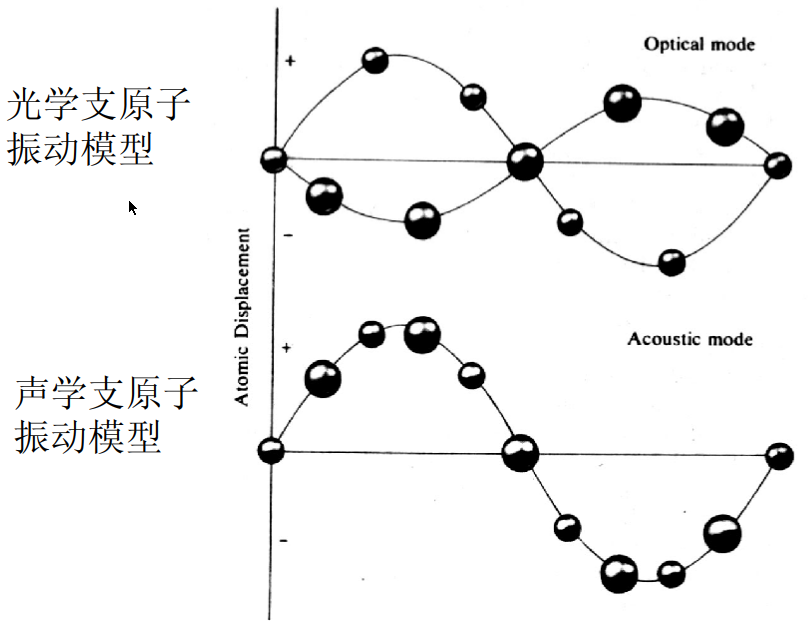 ,
, - 态密度函数(PDOS):单位频率间隔内的状态数(振动模式数目),与声子色散关系的关联,看这里
本文作者:yuhldr
本文地址: [https://yuhldr.github.io/posts/9553fedc.html](https://yuhldr.github.io/posts/9553fedc.html)
版权声明:转载请注明出处!